什么是定点数
通俗的解释
定点数指小数点在数中的位置是固定不变的,通常有定点整数和定点小数。在对小数点位置作出选择之后,运算中的所有数均应统一为定点整数或定点小数,在运算中不再考虑小数问题。
以人民币为例,我们日常经常说到的如123.45¥,789.34¥等等,默认的情况下,小数点后面有两位小数,即角,分。如果小数点在最高有效位的前面,则这样的数称为纯小数的定点数,如0.12345,0.78934等。如果小数点在最低有效位的后面,则这样的数称为纯整数的定点数,如12345,78934等。
专业的说法
所谓定点格式,即约定机器中所有数据的小数点位置是固定不变的。通常将定点数据表示成纯小数或纯整数,为了将数表示成纯小数,通常把小数点固定在数值部分的最高位之前;而为了将数表示成纯整数,则把小数点固定在数值部分的最后面,如下图所示:
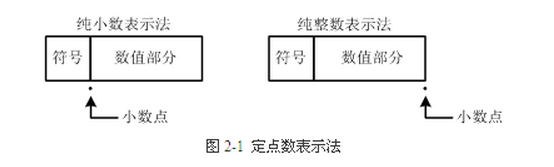
什么是浮点数
通俗的解释
浮点数:一般说来,小数点不固定的数。比较容易的理解方式是,考虑以下我们日常见到的科学记数法,拿我们上面的数字举例,如123.45,可以写成以下几种形式
如:
12.345x10^1^
1.2345 x10^2^
0.12345 x10^3^
……
为了表示一个数,小数点的位置可以变化,即小数点不固定。
专业的说法
定点数表示法的缺点在于其形式过于僵硬,固定的小数点位置决定了固定位数的整数部分和小数部分,不利于同时表达特别大或特别小的数,最终,绝大多数现代的计算机系统采纳了浮点数表达方式,这种表达方式利用科学计数法来表达实数,即用一个尾数(Mantissa,尾数有时也称为有效数字,它实际上是有效数字的非正式说法),一个基数(Base),一个指数(Exponent)以及一个表示正负的符号来表达实数,比如123.45用十进制科学计数法可以表示为1.2345x10^2^,其中1.2345为尾数,10为基数,2为指数。浮点数利用指数达到了浮动小数点的效果,从而可以灵活地表达更大范围的实数。
定点数与浮点数的对比
定点表示法运算直观,但数的表示范围较小,不同的数运算时要考虑比例因子的选取,以防止溢出。浮点表示法运算时可以不考虑溢出,但浮点运算,编程较难。要掌握定、浮点数的转换方法及浮点数规格化方法。
表示的精度与范围不同
例如,我们用4个十进制数来表达一个数字。对于定点数(这里以定点整数为例),我们表示区间[0000,9999]中的任何一个数字,但是如果我们要想表示类似1234.3的数值就无能为力了,因为此时的表示精度为1/10^0^=1;如果采用浮点数来表示(以归整的科学记数法,即小数点前有一位有效位,为例),则可以表示[0.000,9.999]之间的任何一个数字,表示的精度为1/10^3^=0.001,精度比上一种方式提高了很多,但是表示的范围却小了很多。
也就是说,一般的,定点数表示的精度较低,但表示的数值范围较大;而浮点数恰恰相反。
计算机中运算的效率不同
一般说来,定点数的运算在计算机中实现起来比较简单,效率较高;而浮点数的运算在计算机中实现起来比较复杂,效率相对较低。
硬件依赖性
一般说来,只要有硬件提供运算的部件,就会提供定点数运算的支持(不知道说的确切否,没有听说过不支持定点数运算的硬件),但不一定支持浮点数运算,如有的很多嵌入式开发板就不提供浮点运算的支持。
浮点数的存储格式
IEEE 浮点格式规范
浮点数的小数点是不固定的,如果每个人都按照自己的爱好存储在电脑里,那不就乱套了吗?那么怎么在计算机中存储这种类型的数字呢?象这类古老的问题前人早都为我们做好了相应的规范,无规矩不成方圆吗。我们平时所说的浮点数的存储规范,就是由IEEE指定的,具体的规范文件是:IEEE Standard 754 for Binary Floating-Point Arithmetic。大家可以很容易的从网络上下载到这篇文档。
单精度浮点
在c语言中,单精度(float)数据类型为32bits,具体的如下图所示:

整个32bits分三部分,即
Sign:符号位,1 bit,0为正,1为负;
Exponent(bias):指数部分,8 bits,存储格式为移码存储(后面还会说明),偏移量为127;
Mantissa(fraction):尾数部分。
双精度浮点
对应的双精度(double)类型的格式为:
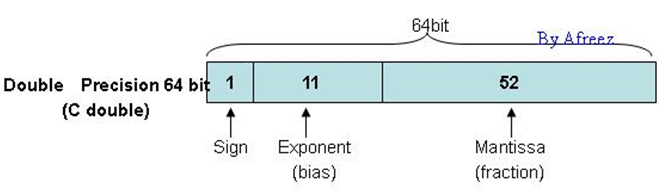
同样,64位也被分为了三部分,对照单精度,不用我说就可以理解各个部分的含义了吧?
是不是有点迷糊了,不要怕,理论这个东西最能忽悠人了,看起来很高深,其实也就是个屁大的事,举个例子就很容易明白了。
举例说明,如3.24x10^3^,则对应的部分为,Sign为0,3为指数部分(注意计算机里面存储的不是3,这里仅仅为了说明),3.24为尾数。我们知道,计算机“笨”的要死,只认识0和1,那么到底一个浮点数值在计算机存储介质中是如何存储的呢?
例如,我们要想偷窥浮点类型的值4.25在计算机硬盘中存储的庐山真面目,请跟我来:首先把4.25转换成二进制的表达方式,即100.01,在详细点,变成1.0001x2^2^,好了,对号入座把。
Sign=0;
Exponent(bias)=2+127=129 (偏移量为127,就是直接加上个127了);
Mantissa=1.0001-1.0=0001(规格化后,小数点前总是整数1,全世界人都知道前面是1不是0,所以省略不写了,即尾数部分不包括整数部分;当别人问你,为什么23 bit的尾数部分可以表示24位的精度,知道怎么回答了吧。 靠,什么,没有看懂,再仔细读两便就知道了)。
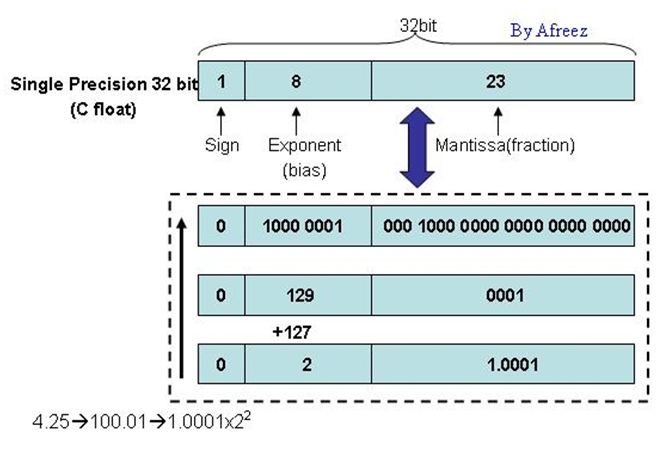
对照上面的图示,相信你已经看明白了吧?相信你的智商。为了加深认识,再来一个。如果给定你一个二进制数字串
01000000100010000000000000000000
并告诉你这是一个float类型的值,让你说出它是老几,知道怎么算了吧?如果不知道,看下面的图,我就不废话解释了。
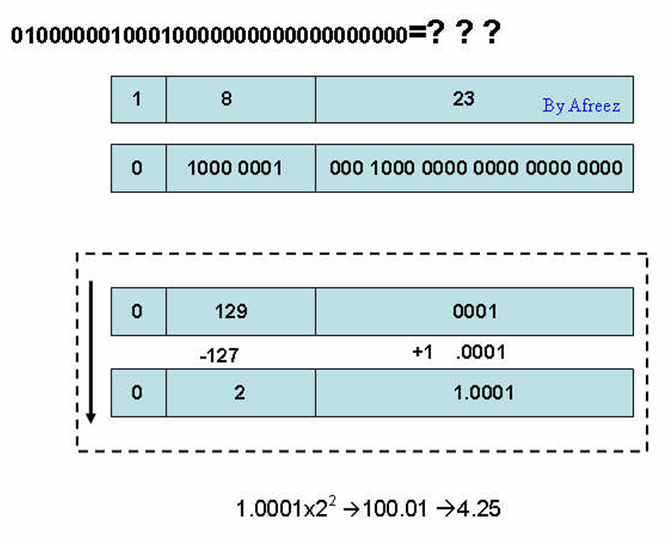
浮点定点转换
Q格式定标法
通过假定小数点位于哪一位(Q)的右侧,从而确定小数的精度,以下为32位数Q定标表格。
| Q表示 | 十进制浮点数表示范围 | 精度 |
|---|---|---|
| Q=31 | -1≤x≤0.999 999 999 | 2^(-31) |
| Q=30 | -2≤x≤1.999 999 999 | 2^(-30) |
| Q=29 | -4≤x≤3.999 999 998 | 2^(-29) |
| Q=28 | -8≤x≤7.999 999 996 | 2^(-28) |
| Q=27 | -16≤x≤15.999 999 993 | 2^(-27) |
| Q=26 | -32≤x≤31.999 999 985 | 2^(-26) |
| Q=25 | -64≤x≤63.999 999 970 | 2^(-25) |
| Q=24 | -128≤x≤127.999 999 940 | 2^(-24) |
| Q=23 | -256≤x≤255.999 999 981 | 2^(-23) |
| Q=22 | -512≤x≤511.999 999 762 | 2^(-22) |
| Q=21 | -1024≤x≤1023.999 999 523 | 2^(-21) |
| Q=20 | -2048≤x≤2047.999 999 046 | 2^(-20) |
| Q=19 | -4096≤x≤4095.999 998 093 | 2^(-19) |
| Q=18 | -8192≤x≤8191.999 996 185 | 2^(-18) |
| Q=17 | -16384≤x≤16363.999 992 371 | 2^(-17) |
| Q=16 | -32768≤x≤32767.999 984 741 | 2^(-16) |
| Q=15 | -65536≤x≤65535.999 969 482 | 2^(-15) |
| Q=14 | -131072≤x≤131071.999 938 965 | 2^(-14) |
| Q=13 | -262144≤x≤262143.999 877 930 | 2^(-13) |
| Q=12 | -5244288≤x≤524287.999 755 859 | 2^(-12) |
| Q=11 | -1048576≤x≤1048575.999 511 719 | 2^(-11) |
| Q=10 | -2097152≤x≤2097151.999 511 719 | 2^(-10) |
| Q=9 | -4194304≤x≤4194302.998 046 875 | 2^(-9) |
| Q=8 | -8388608≤x≤8388607.996 093 750 | 2^(-8) |
| Q=7 | -16777216≤x≤16777215.992 187 500 | 2^(-7) |
| Q=6 | -33554432≤x≤33554431.984 375 000 | 2^(-6) |
| Q=5 | -67108864≤x≤67108863.968 750 000 | 2^(-5) |
| Q=4 | -134217728≤x≤134217727.937 500 000 | 2^(-4) |
| Q=3 | -268435456≤x≤268435455.875 000 000 | 2^(-3) |
| Q=2 | -536870912≤x≤536870911.750 000 000 | 2^(-2) |
| Q=1 | -1073741824≤x≤1073741823.500 000 000 | 2^(-1) |
| Q=0 | -2147483648≤x≤2147483647 | 2^0 |
转换关系
浮点数(X)转换为定点数(Xq):Xq=(int)X* 2^Q
定点数(Xq)转换为浮点数(X):X=(float)Xq*2^(-Q)
Example:
将浮点数X = 0.5转换为32位Q定标的定点数:
(1)由于-1≤X≤0.999 999 999,按照上述表格所以我们取Q = 31,
即定点数:Xq=(int)X 2^Q = (int)(0.5 2^31) = 1073741842;
反之知道定点数Xq = 1073741842 反推其浮点数如下
则X=(float)Xq2^(-Q) = (float)10737418422^(-31) = 0.5;
按照上述如果我们取Q = 31,如果我们要计算浮点的0.50.5,则相当于计算定点的1073741842 1073741842 这个数实在是太大了,只能用long long型装下,而非一个字(int)可以装下。通过观察0.5这个数我们只需要保证表格中的Q值对应的精度比0.5更小即可,如此我们重新选择Q:
(2)由于-536870912≤x≤536870911.750 000 000,按照上述表格我们取Q = 2, 即定点数:Xq=(int)X 2^Q = (int)(0.5 2^2) = 2; 反之知道定点数Xq = 2 反推其浮点数如下 则X=(float)Xq2^(-2) = (float)22^(-2) = 0.5; 按照上述如果我们取Q = 2,如果我们要计算浮点的0.50.5,则相当于计算定点的2 2,一个char就可以装下了。
